Chapter 3 Problems

1

The moment arm on our gravity force will equal $\cos(30^\circ)(0.3\text m)$, so to balance our torques, we have $$(.02\text m)F_\text{tendon} = \cos(30^\circ)(0.3\text m)(3\text{kg})\left(9.81\text{m/s}^2\right).$$ Isolating the petella force here gives $$F_\text{tendon} = \frac{\cos(30^\circ)(0.3\text m)(3\text{kg})\left(9.81\text{m/s}^2\right)}{.02\text m} = \boxed{382.3\text N}.$$

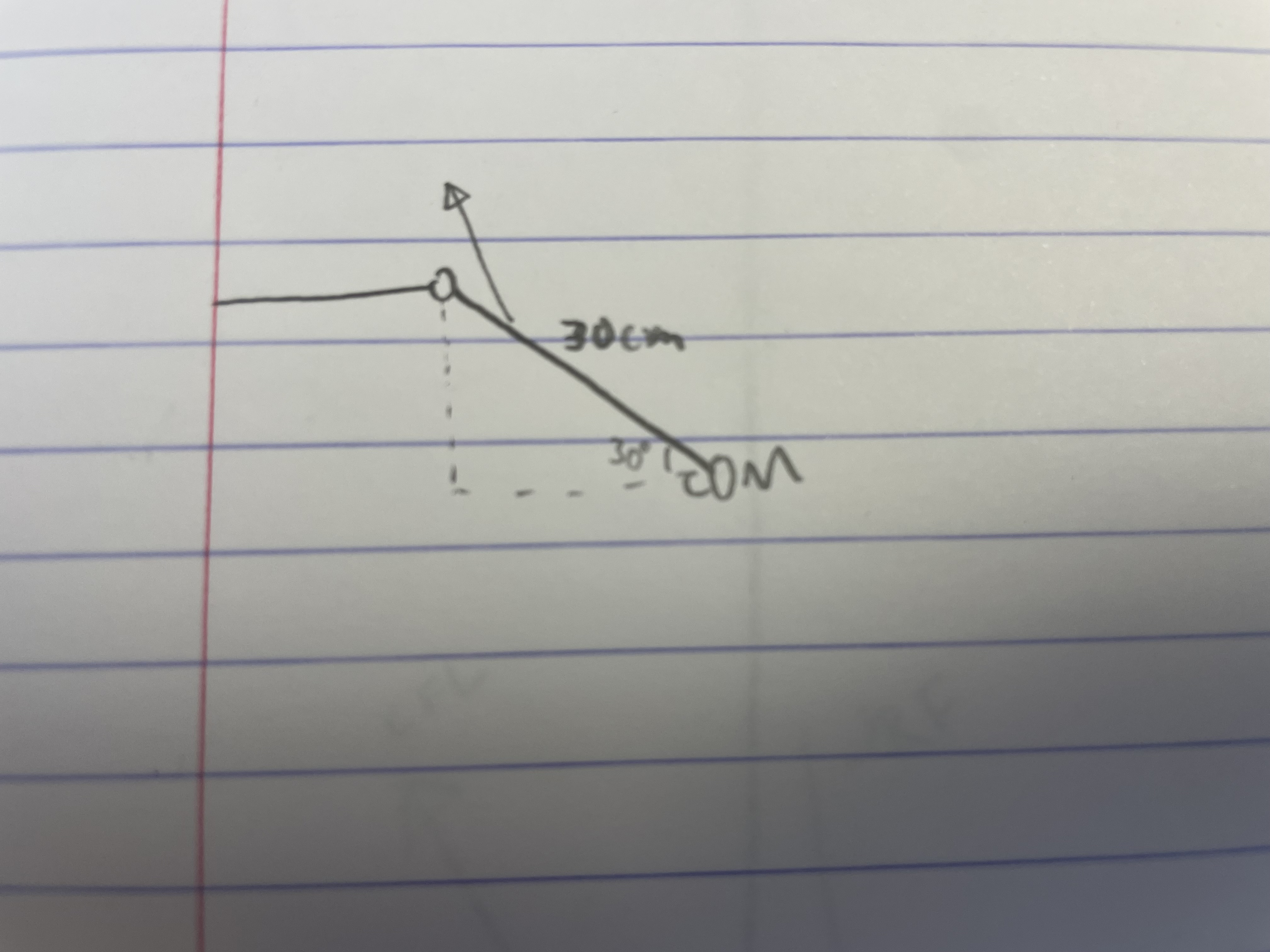
2

A.

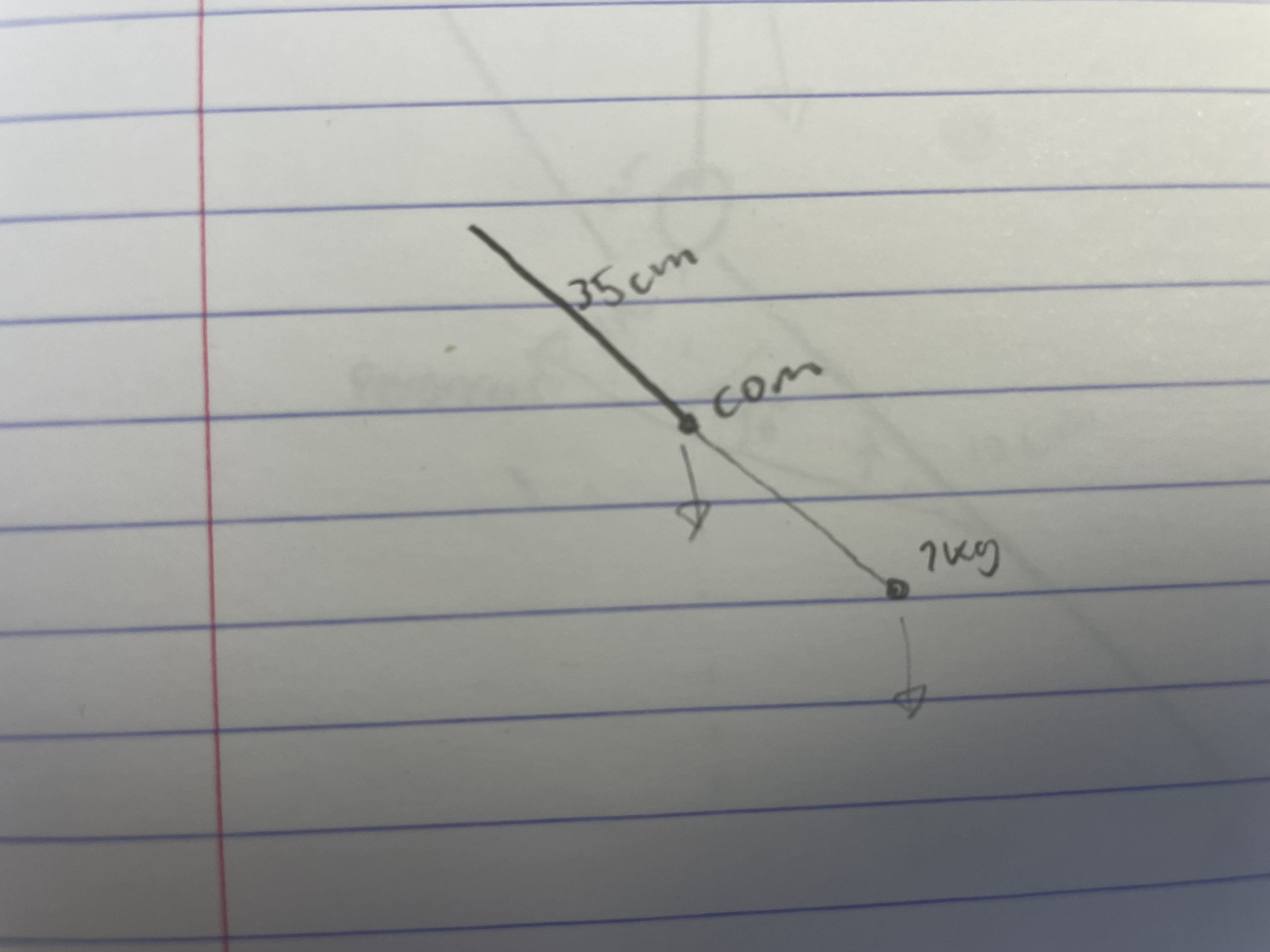
B. The moment arm of the COM will be $\sin(60^\circ)(.35\text m)$, and the moment arm of the dumbell will be $\sin(60^\circ)(.7\text m)$. Therefore, their combined torques will be $$\sin(60^\circ)(.35\text m)(5\text{kg})\left(9.81\text{m/s}^2\right) + \sin(60^\circ)(.7\text m)(7\text{kg})\left(9.81\text{m/s}^2\right).$$ Setting the total torque equal to zero gives $$(.02\text m)F_\text{deltoid} = \sin(60^\circ)(.35\text m)(5\text{kg})\left(9.81\text{m/s}^2\right) + \sin(60^\circ)(.7\text m)(7\text{kg})\left(9.81\text{m/s}^2\right).$$ Isolatin the deltoid force gives $$F_\text{deltoid} = \frac{\sin(60^\circ)(.35\text m)(5\text{kg})\left(9.81\text{m/s}^2\right) + \sin(60^\circ)(.7\text m)(7\text{kg})\left(9.81\text{m/s}^2\right)}{.02\text m} = \boxed{2824.8\text N}.$$

C. The force of the deltoid is being applied at $10^\circ$ less than the $60^\circ$ humerus, or in other words at $50^\circ$ from vertical, the $x$-component of $F_\text{deltoid}$ will be $$\sin(50^\circ)2824.8\text N = 2163.9\text N$$ and the $y$-component will be $$\cos(50^\circ)2824.8\text N.$$ Since the total force in the $y$ direction is $$\cos(50^\circ)2824.8\text N - (5\text{kg})\left(9.81\text{m/s}^2\right) - (7\text{kg})\left(9.81\text{m/s}^2\right) = 1698.0\text N,$$ the joint reaction force is $$\text{JRF} = \begin{pmatrix}2163.9\text N \\ 1698.0\text N\end{pmatrix}$$

D. The $x$ component of the latissimus force would add to the deltoid, but the $y$ component would subtract. The JRF would increase overall, but there would be less superior translation of the humerus, likely leading to greater joint stability.

3

A.

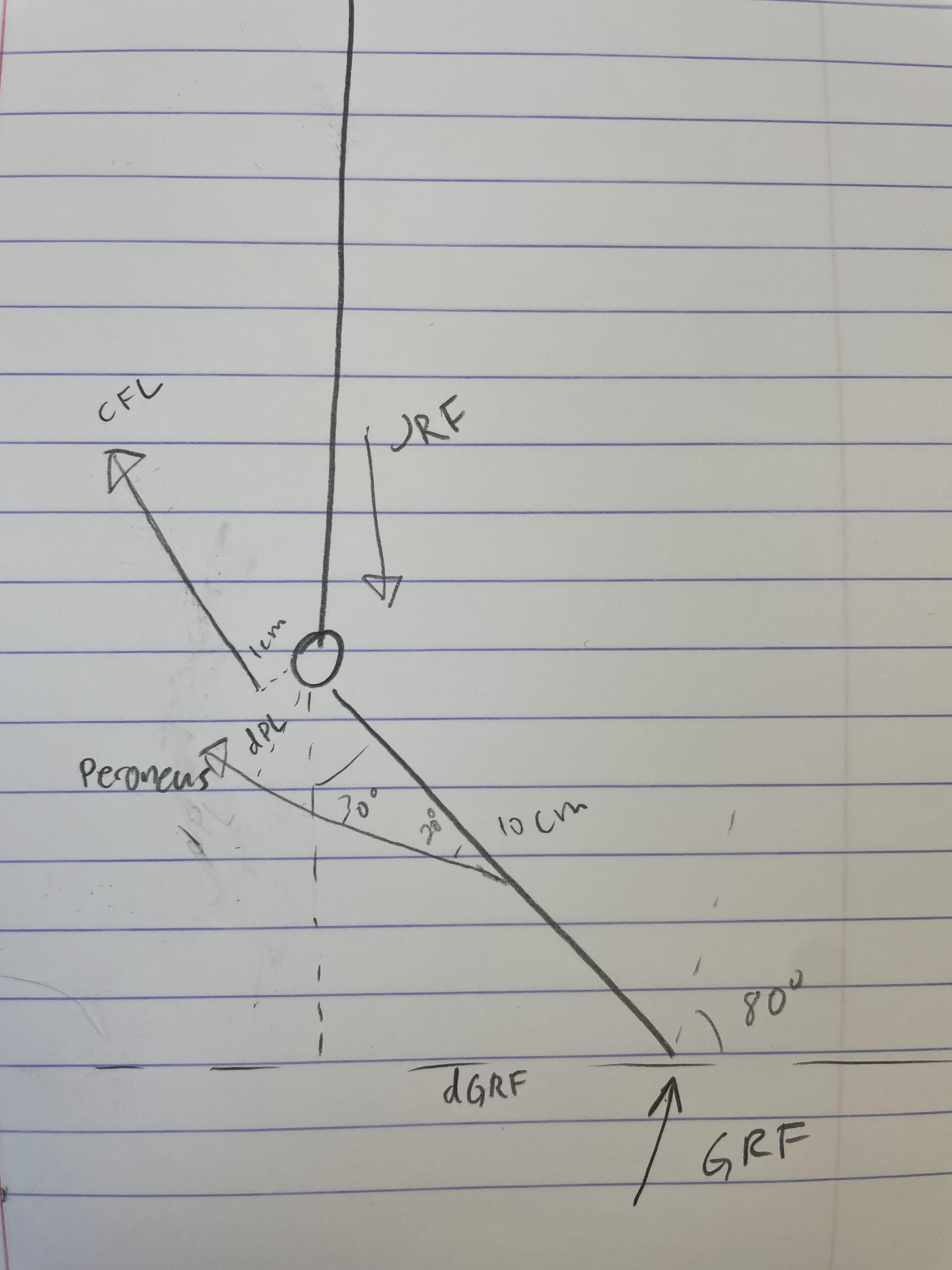
B. The moment arm of the ground reaction force will be $$\sin(30^\circ)(.1\text m) = .05\text m,$$ and the moment arm of the peroneus will be $$\sin(40^\circ)(.1\text m) \approx .064\text m.$$

C. If the net torque is zero, then $$\sin(30^\circ)(.1\text m)(1500\text N) = \sin(40^\circ)(.1\text m)(1800\text N) + (.01\text m)(\text F_\text{CFL}).$$ Rearranging gives $$F_\text{CFL} = \frac{\sin(30^\circ)(.1\text m)(1500\text N) - \sin(40^\circ)(.1\text m)(1800\text N)}{.01\text m} = \boxed{4070.2\text N}.$$

D. No, the force of $4070.2\text N$ does not exceed $5000\text N$.

E.

F.