Chapter 8 problems

Problem 1

This problem should look familiar. We’ve simply added a twist to it in that now you can do it under two conditions, isometric, and concentric contractions. A PT is rehabbing the knee of a patient recovering from ACL reconstruction surgery in which the surgeon used the middle third of the patella tendon as a graft. Therefore, there is a concern about high levels of force on the patella tendon. The PT has the patient extend her knee against the resistance force of gravity. The patient is sitting upright with her hips in 90 degrees of flexion. You are asked to determine the difference in quadriceps force (ie, force on the patella tendon) between an isometric and concentric exercise. Here is what you know about the patient:
Mass of lower leg (m) = 3 kg
Length of lower leg (D) = 50 cm
Distance from COR of knee to COM of leg (L) = 30 cm
Radius of gyration from COR (k) = 38 cm
Moment arm of patella tendon (T) = 2 cm
Knee flexion angle = 30 degrees
Extension angular acceleration for concentric exercise = 1000 degrees/sec2

a) Draw an appropriate free body diagram for this problem – make sure all of the appropriate forces are clearly labeled.

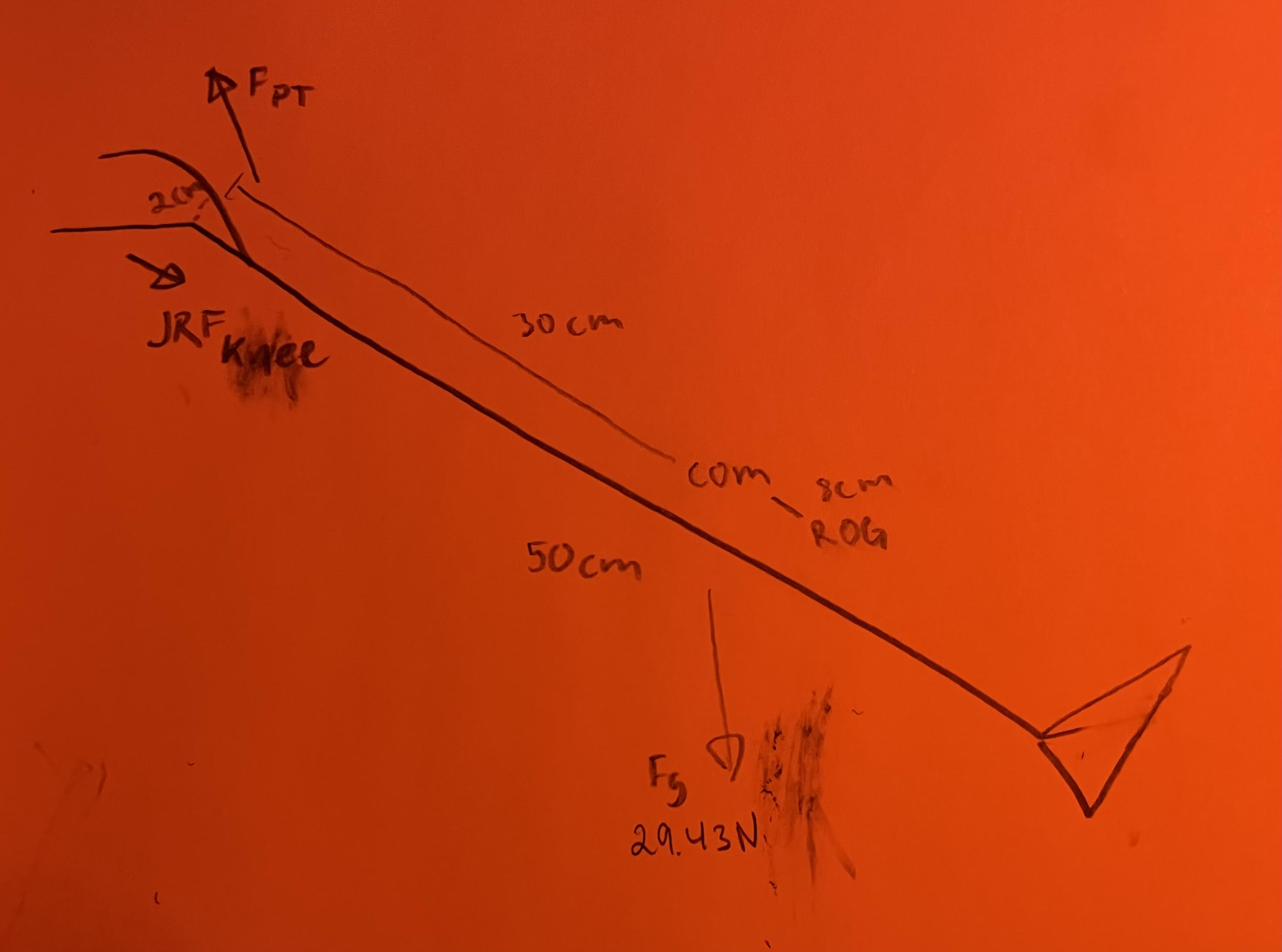
b) Solve for the force on the patella tendon (do not plug in numbers at this point).

$$ F_\text{PT} \cdot d_\text{PT} + F_\text{g} \cdot d_\text{COM} = I_\text{\text{leg}}\cdot \text{ (angular acceleration)}, $$ Therefore, $$ F_\text{PT} = \frac{I_\text{\text{leg}}\cdot \text{ (angular acceleration)} - F_\text{g} \cdot d_\text{COM}}{d_\text{PT}}. $$

c) Calculate the force under both isometric (no acceleration) and concentric (acceleration as noted above) conditions.

We have $$ d_\text{COM} = \cos(30^\circ)\cdot 0.3\text{ m} \approx 0.2598\text{ m}, $$ $$\alpha_\text{concentric} \approx 17.45\text{ rad/s}^2, $$ $$ F_g = -29.43\text{ N}, $$ $$ I_\text{leg} = 3\text{ kg}\cdot (0.38\text{ m})^2 = 0.4332\text{ kg m}^2. $$

isometric: $$ F_\text{PT} = \frac{-(-29.43\text{ N})\cdot 0.2598\text{ m}}{0.02\text{ m}} \approx 382.30\text{ N} $$

concentric $$ F_\text{PT} = \frac{0.4332\text{ kg m}^2 \cdot 17.45\text{ rad/s}^2 -(-29.43\text{ N})\cdot 0.2598\text{ m}}{0.02\text{ m}} \approx 760.26\text{ N} $$

d) Based on these results, comment on the consequences of performing this activity with a non-zero acceleration?

The quadriceps force doubles (from 382 N to 760 N) when moving from isometric to concentric contraction with the given acceleration. This means higher stress on the patellar tendon graft, which could risk graft failure or impede healing if the patient is not ready for such loading. Early-stage rehab should focus on isometric or slow, controlled movements to minimize patellar tendon forces. Accelerated movements (e.g., rapid extensions) should be avoided until the tendon has sufficiently healed.

Problem 2

When punting, a good goalie achieves a hip angular acceleration of 1000 degrees/sec2 at the time of impact with the ball. For this problem, you will be calculating the hip flexor force necessary for this task.
The following are given:
Height of the athlete when standing upright = 1.85 m
Mass of the athlete = 85 kg
Weight of soccer ball is negligible
Knee is in full extension, ankle in full plantarflexion
Weight of leg (FW) = ? N
Distance from hip COR to leg COM (LW) = ? cm
Force of contact with ball (FB ) = 100 N (perpendicular to shank)
Distance from hip COR to point of contact with ball (LB ) = ? cm
Radius of gyration for leg (k) = ? cm
Hip flexor moment arm (MAH) = 6.5 cm
Hip flexion angle (θ) = 25° down from horizontal/65° up from vertical
Angular hip flexion acceleration (α) = 1500 degrees/sec2 → (?? rad/sec2 )

a) Use the anthropometric table and stature chart on the following pages to determine the length of the athlete’s kicking leg, the mass of the leg (treat the leg as a single segment), the location of the leg’s center of mass, and the moment of inertia for the leg.

Length of the kicking leg: $$ 0.53\cdot 1.85\text{ m} = \boxed{0.9805\text{ m}} $$

Mass of the leg: $$ m = 0.161\cdot 85\text{ kg} = \boxed{13.685\text{ kg}} $$

Location of the leg’s COM: $$ 0.447\cdot 13.685\text{ kg} \approx \boxed{6.117\text{ m}}\text{ (distal from the greater trochanter.)} $$

Moment of inertia for the leg: $$ I_\text{LE} = 13.685\text{ kg}\cdot (0.560 \cdot 0.9805\text{ m})^2 \approx \boxed{4.126 \text{ kg m}^2} $$

b) Based on the stick figure shown above at right, draw a free body diagram for this problem.

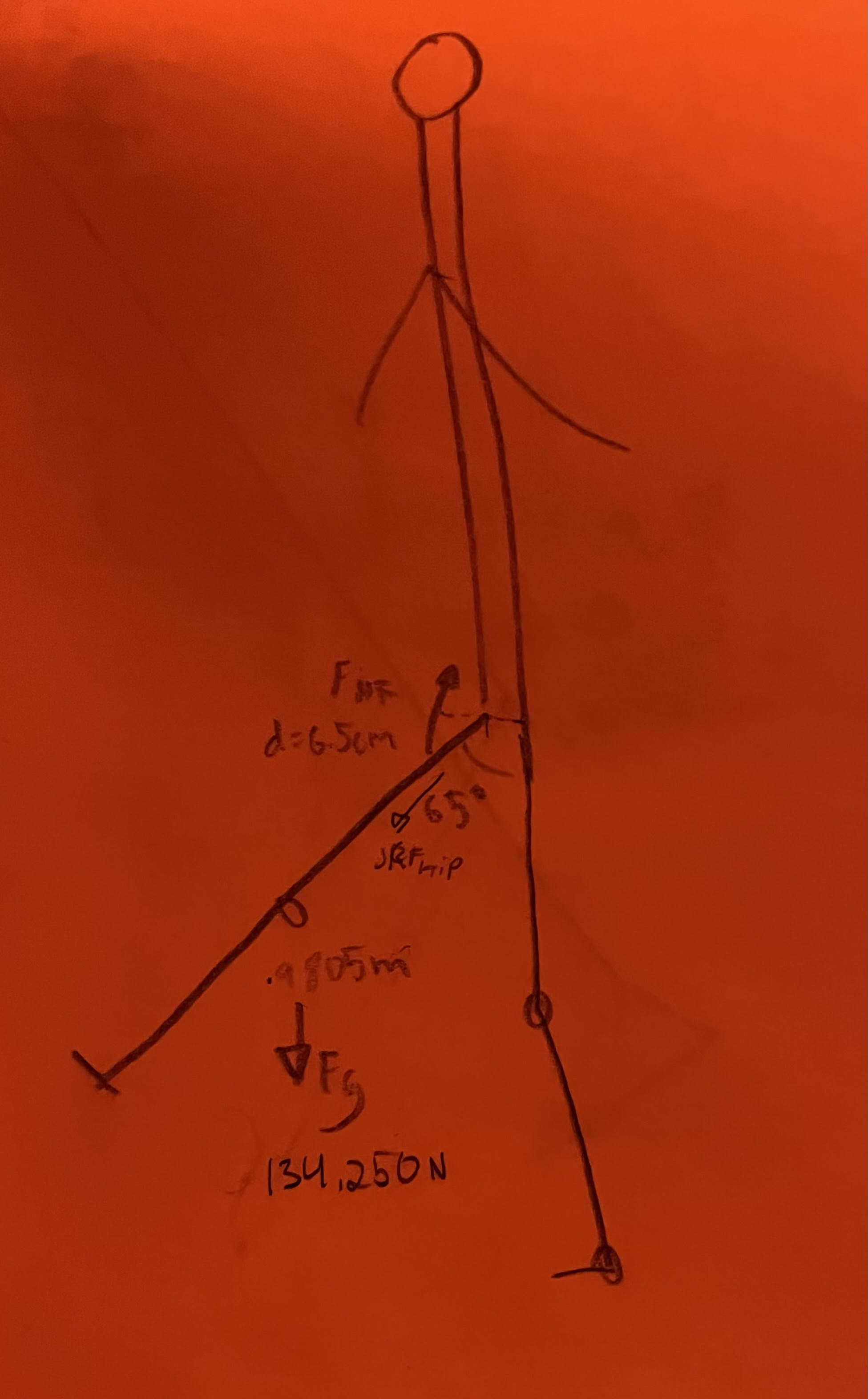
c) Solve for the hip flexor muscle force required for the goalie to generate this hip angular acceleration.

We would like to find the hip flexor force $F_\text{HF}$. We know that the sum of the torques $$ \Tau_g + \Tau_\text{ball} + \Tau_{HF} = I_\text{LE}\cdot \alpha, $$ We can now rewrite this as $$ F_g\cdot d_g + F_\text{ball} \cdot d_\text{ball} + F_\text{HF}\cdot d_\text{HF} = I_\text{LE}\cdot \alpha. $$ which rearranges to $$ F_\text{HF} = \frac{I_\text{LE}\cdot \alpha - F_g\cdot d_g + F_\text{ball} \cdot d_\text{ball}}{d_\text{HF}}. $$ Using our calculations from part a, we have $$ F_\text{HF} = \frac{4.126 \text{ kg m}^2\cdot 26.18\text{ rad/s}^2 - (-134.25\text{ N})\cdot 6.117\text{ m} + 100\text{ N} \cdot 0.9805\text{ m}}{0.065\text{ m}}. $$ Evaluating this gives $$ F_\text{HF} \approx \boxed{15804\text{ N}}. $$

d) After a month of training, this player has been able to double his punt distance by doubling his angular acceleration to 3000 degrees/sec2 . Verify that this change doubles the linear acceleration of the goalies foot at the time of impact with the ball.

If we ignore the centripetal acceleration $a_c$ and only focus on tangential acceleration $a_t$, then we see that $$ a_t = r\cdot\alpha, $$ where $r$ is the radius from the center of rotation. Therefore, doubling $\alpha$ would also double $a_t$.

However, if we take angular velocity $\omega$ in to account, then we will have $$ a = a_c+a_t = \sqrt{(r\alpha)^2+(r\omega^2)^2}, $$ and this linear relationship no longer holds if $\omega \neq 0$.

e) Solve for the new muscle force.

This time, we have $$ F_\text{HF} = \frac{4.126 \text{ kg m}^2\cdot 52.36\text{ rad/s}^2 - (-134.25\text{ N})\cdot 6.117\text{ m} + 100\text{ N} \cdot 0.9805\text{ m}}{0.065\text{ m}}. $$ Evaluating this gives $$ F_\text{HF} \approx \boxed{17466\text{ N}}. $$

f) Does the doubling of angular acceleration require a doubling of the muscle force? Why or why not?

Doubling the angular acceleration did not require a doubling of muscle force because the muscle force is not the only force acting on the lower extremity. Therefore, $F_\text{HF}$ does not equal $\alpha$ times some constant. To see why this must obviously be true, note that there is a non-zero value of $F_\text{HF}$ for which $\alpha$ will be zero.

Chapter 8 HW Chap 10 HW